Polyiamonds attaining extremal topological properties, part 2

Abstract

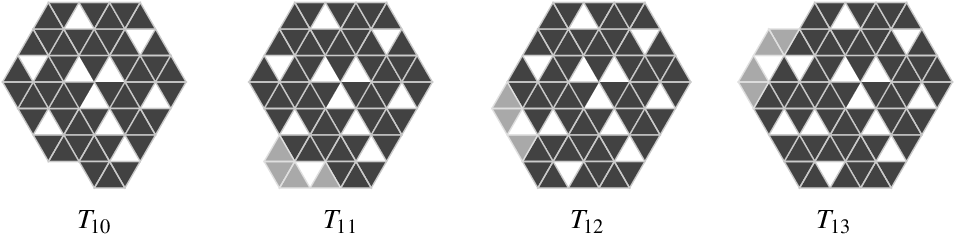
In Part II of this work we construct crystallized polyiamonds with $h$ holes for every $h\ge 1$, that is polyiamonds which use the fewest possible tiles necessary to enclose $h$ holes. Furthermore, we prove that crystallized polyiamonds satisfy a set of structural conditions, and for every $h\ge 3$ there are multiple distinct crystallized polyiamonds with $h$ holes.