Moduli spaces of morse functions for persistence

Abstract

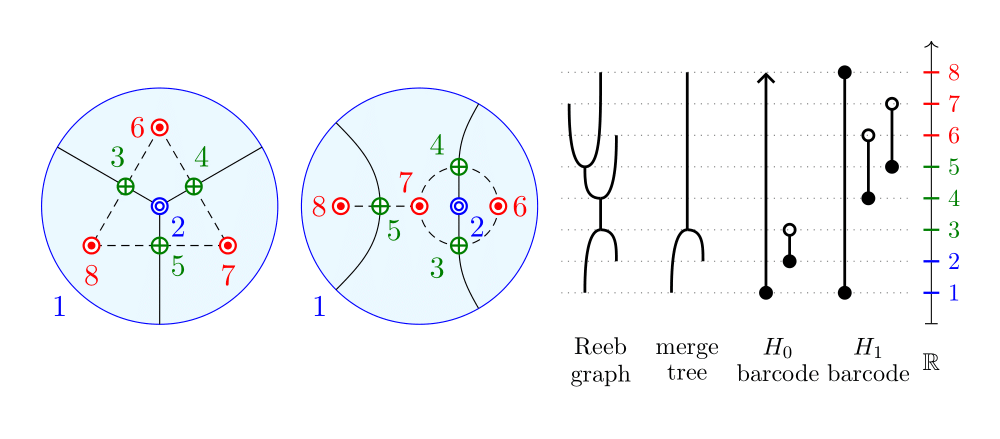
We consider different notions of equivalence for Morse functions on the sphere in the context of persistent homology and introduce new invariants to study these equivalence classes. These new invariants are as simple–but more discerning than–existing topological invariants, such as persistence barcodes and Reeb graphs. We give a method to relate any two Morse–Smale vector fields on the sphere by a sequence of fundamental moves by considering graph-equivalent Morse functions. We also explore the combinatorially rich world of height-equivalent Morse functions, considered as height functions of embedded spheres in $R^3$. Their level set invariant, a poset generated by nested disks and annuli from level sets, gives insight into the moduli space of Morse functions sharing the same persistence barcode.