Extremal {p,q}-Animals

Abstract

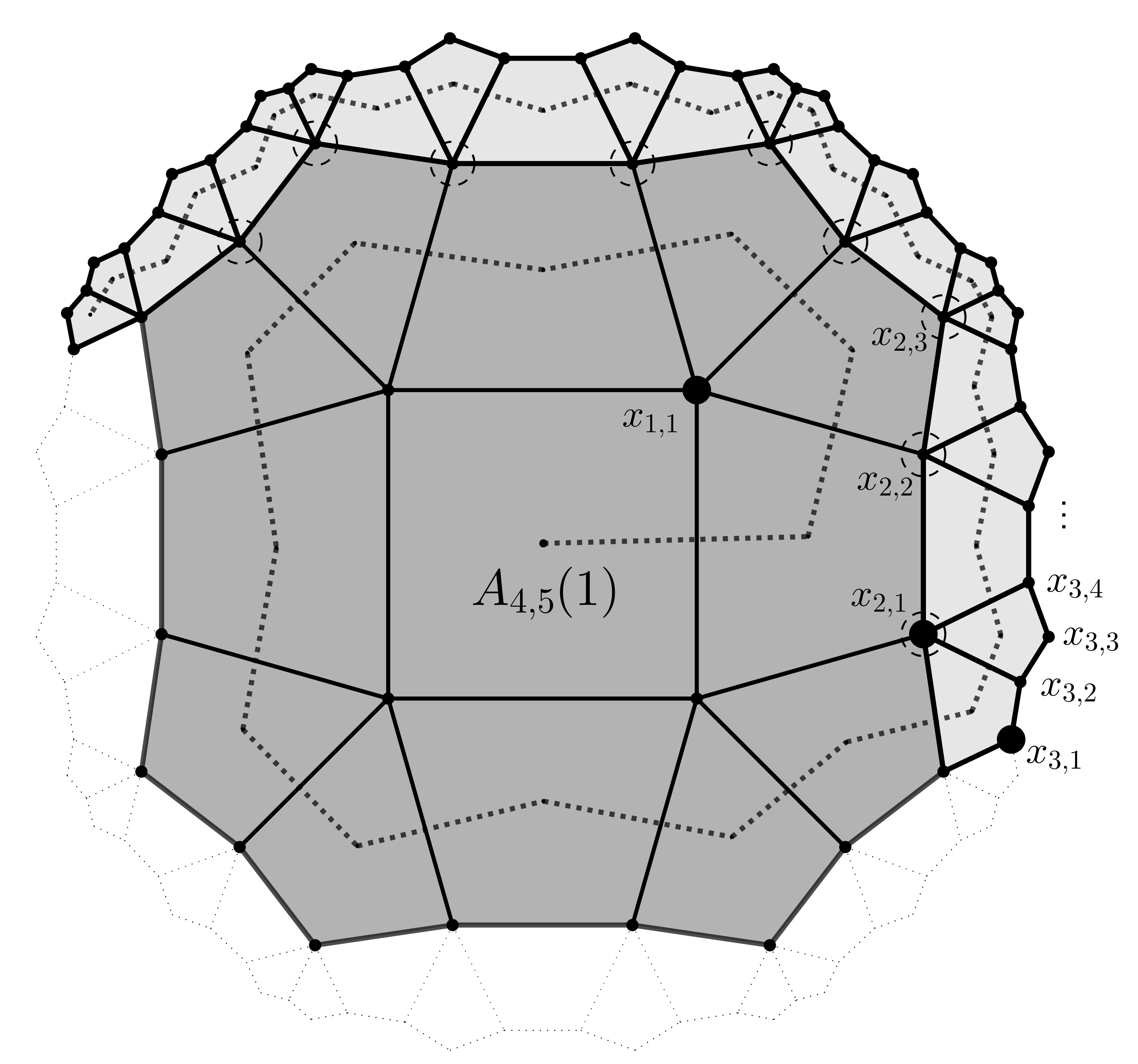
An animal is a planar shape formed by attaching congruent regular polygons along their edges. Usually, these polygons are a finite subset of tiles of a regular planar tessellation. These tessellations can be parameterized using the Schläfli symbol {p,q}, where p denotes the number of sides of the regular polygon forming the tessellation and q is the number of edges or tiles meeting at each vertex. If (p-2)(q-2)> 4, =4, or <4, then the tessellation corresponds to the geometry of the hyperbolic plane, the Euclidean plane, or the sphere, respectively. In 1976, Harary and Harborth studied animals defined on regular tessellations of the Euclidean plane, finding extremal values for their vertices, edges, and tiles, when any one of these parameters is fixed. They named animals attaining these extremal values as extremal animals. Here, we study hyperbolic extremal animals. For each {p,q} corresponding to a hyperbolic tessellation, we exhibit a sequence of spiral animals and prove that they attain the minimum numbers of edges and vertices within the class of animals with $n$ tiles. We also give the first results on enumeration of extremal hyperbolic animals by finding special sequences of extremal animals that are unique extremal animals, in the sense that any animal with the same number of tiles which is distinct up to isometries cannot be extremal.